In algebra, summation is a well-known technique used for denoting the sum of the list of observations or numbers. The summation is frequently used in central tendency and many other daily life problems for evaluating the sum of various terms.
Simple summation is used to find the sum of a list of numbers while the summation notation is used to wind up the list of numbers. In this lesson, we will learn all the basics of summation notation along with a lot of examples.
What is summation?
In algebra, summation is a term that is used to denote the sum of the list of numbers or used to calculate the list of numbers (long addition). The notation used in summation for representing the numbers of long addition is known as sigma notation.
In mathematics, the summation is used to find the algebraic sum of squares. While in statistics, the summation is used in central tendency and for finding the statistical sum of squares. It is denoted by the Greek notation “∑” and read as sigma notation or summation notation.
Equation of summation
Here is the general equation of the summation.
Summation notation formula:
For summation notation

For simple summation notation:
Simple summation is the form of long addition
Simple summation = x1 + x2 + x3 + … + xn
Laws of sigma notation
Here are the basic laws of summation notation that are used to calculate the problems of the summation.
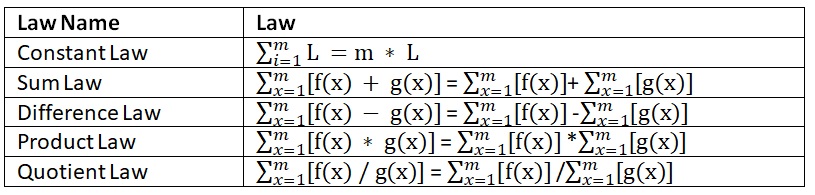
How to solve the problems of summation?
Let us take a few examples of simple summation and summation notation. The first example is for the simple summation while the other is for the summation notation that is solved by two methods.
Example 1: For simple summation
Find the summation of the given list of numbers.
1, 12, 16, 18, 19, 20, 25
Solution
Step 1: First of all, take the given list of numbers and add the addition sign among each number.
List of numbers = 1, 12, 16, 18, 19, 20, 25
Simple summation = 1 + 12 + 16 + 18 + 19 + 20 + 25
Step 2: Now add the above expression according to the long addition method.
= 1 + 12 + 16 + 18 + 19 + 20 + 25
= 13 + 16 + 18 + 19 + 20 + 25
= 29 + 18 + 19 + 20 + 25
= 47 + 19 + 20 + 25
= 66 + 20 + 25
= 86 + 25
= 111
What is summation notation Calculator?
A summation notation calculator can be used to solve the problems of simple summation as well as sigma notation.
Example 2: For sigma notation
Calculate the summation of the given function with the initial value 1 and the final value 6.
f(x) = 2x3 – 3x2 +9
Solution
Step 1: First of all, write the notation of summation to the given function.
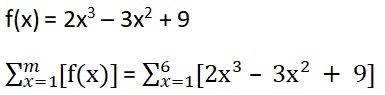
Step 2:Now place the values of x from 1 to 6,in the given expression.
For x= 1
2x3 – 3x2 + 9 = 2(1)3 – 3(1)2 + 9
2x3 – 3x2 + 9 = 2(1) – 3(1) + 9
2x3 – 3x2 + 9 = 2 – 3 + 9
2x3 – 3x2 + 9 = 8
For x= 2
2x3 – 3x2 + 9 = 2(2)3 – 3(2)2 + 9
2x3 – 3x2 + 9 = 2(8) – 3(4) + 9
2x3 – 3x2 + 9 = 16 – 12 + 9
2x3 – 3x2 + 9 = 13
For x= 3
2x3 – 3x2 + 9 = 2(3)3 – 3(3)2 + 9
2x3 – 3x2 + 9 = 2(27) – 3(9) + 9
2x3 – 3x2 + 9 = 54 – 27 + 9
2x3 – 3x2 + 9 = 36
For x= 4
2x3 – 3x2 + 9 = 2(4)3 – 3(4)2 + 9
2x3 – 3x2 + 9 = 2(64) – 3(16) + 9
2x3 – 3x2 + 9 = 128 – 48 + 9
2x3 – 3x2 + 9 = 89
For x= 5
2x3 – 3x2 + 9 = 2(5)3 – 3(5)2 + 9
2x3 – 3x2 + 9 = 2(125) – 3(25) + 9
2x3 – 3x2 + 9 = 250 – 75 + 9
2x3 – 3x2 + 9 = 184
For x= 6
2x3 – 3x2 + 9 = 2(6)3 – 3(6)2 + 9
2x3 – 3x2 + 9 = 2(216) – 3(36) + 9
2x3 – 3x2 + 9 = 432 – 108 + 9
2x3 – 3x2 + 9 = 333
Step 3: Now take the sum of all the above-calculated terms.
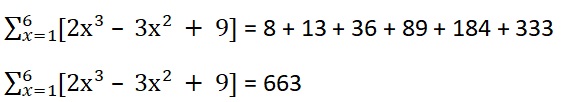
Alternately
Step 1:First of all, apply the sum and difference laws of sigma notation and write the notation of summation to each function separately.


How to solve summation notation?
How to write summation notation:There are two main ways to write summation notation. The first is using the capital Greek letter Σ as sum, which is used to denote summation. The second is using index notation. which is denoted by small letter i.
Summation notation:
Summation notation is a mathematical notation that is used to define the sum of a given sequence. There are two main ways to write summation notation. The first is using the capital Greek letter sigma $\sum$, which is used to denote summation. The second is using index notation.
Index notation is a mathematical notation that uses lettering (usually lowercase letters) to represent numbers. For example, the letter "n" is often used to represent a natural number. Index notation is often used in summation notation because it can be used to represent the sequence of numbers that are being added.
Example of Summation notation:
Here is an example of summation notation using sigma:
$\sum_{i=1}^{n} x_i$
This equation is read as "the sum of x_i from i=1 to n." This equation means that we are adding together all of the x_values from 1 to n. Sigma notation is very useful because it allows us to write out long sums in a concise way.
Here is an example of summation notation using index notation:
$x_1 + x_2 + x_3 + ... + x_n$
This equation is read as "the sum of x_1 plus x_2 plus x_3 up to x_n." This equation means that we are adding together all of the x_values from 1
Final words
Now you can calculate any problem of simple summation and sigma notation by following the above post. We have discussed all the basics of calculating the summation and sigma notation in this post with solved examples.
